Светлана Гин - Мир логики. Программа и методические рекомендации по внеурочной деятельности в начальной школе. Пособие для учителя. 4 класс
• Кирпич весит 1 кг и половину кирпича. Сколько весит кирпич? (2 кг)
• Двое шли, сто рублей нашли. За ними трое идут, сколько они найдут? (Неизвестно, но, скорее всего, – нисколько.)
• Два мальчика играли в шахматы 2 часа. Сколько времени играл каждый? (2 часа)
• Верблюд в течение часа выдерживает ношу в 10 пудов. В течение какого времени он выдержит ношу в 1000 пудов? (Такую ношу он вообще не сможет выдержать.)
9. Подведение итогов занятияЗанятие 15
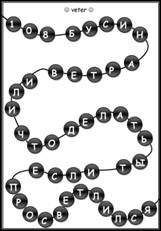
Закономерности в буквах и словах
Правила игры: учитель называет ряд слов: «Апельсин – носорог – гном – мороженое – енот…» – и предлагает детям обнаружить закономерность построения ряда (каждое последующее слово начинается на последнюю букву предыдущего) и продолжить его дальше.
Игра может проходить в быстром темпе на выбывание.
2. Упражнение «Алфавит» (5–7 мин)На доске записаны буквенные ряды. Нужно установить закономерность и продолжить ряд: назвать две следующие буквы.
Примеры рядов букв:
В конце работы – анализ: на какие две группы можно разбить эти ряды.
Например:
1. Ряды, в которых требуется только знание последовательности букв по алфавиту.
2. Ряды, для составления которых требуется не только знание алфавита, но и дополнительные знания (например, о гласных и согласных, о звонких и глухих звуках и т. д.).
3. Работа в группах «Продолжи ряд» (7–8 мин)Каждая группа получает одинаковые ряды слов, в которых нужно найти закономерность построения ряда и дописать следующее слово.
Примеры рядов слов:
1. Молоко – колесо – сода —…
2. Дом – дочь – доска —…
3. Арбуз – бочка – ветер —…
4. Позвонил – поговорил – поранился —…
5. Киев – Воронеж – Жлобин —…
6. Антилопа – актриса – аптека – …
Ответы и комментарии к ним:
1. Закономерность: две последние буквы каждого предыдущего слова и две первые буквы последующего слова – одинаковые. Значит, нужно написать любое слово, начинающееся на «да»: дамба, далеко и т. д.
2. Закономерность: слова начинаются на «до», каждое последующее слово длиннее на одну букву. Значит, нужно написать любое слово из 6 букв, начинающееся на «до»: дорога, домино и т. д.
3. Закономерность: слова из 5 букв, начинающиеся на буквы, следующие по алфавиту. Значит, нужно написать любое слово из 5 букв, начинающееся на «г»: город, гений и т. д.
4. Закономерность: глаголы из 9 букв с приставкой «по». Значит, нужно написать любой глагол из 9 букв с приставкой «по»: поздравил, посмотрел и т. д.
5. Закономерность: города, каждый последующий начинается на последнюю букву предыдущего. Значит, нужно написать любой город, начинающийся на Н: Новгород, Нью-Йорк и т. д.
6. Закономерность: все слова начинаются на А и заканчиваются на А, количество букв уменьшается (8, 7, 6). Значит, нужно написать слово из 5 букв, которое начинается и заканчивается на букву А. Например, афиша, акула.
В конце – обсуждение результатов всех групп и составление краткой инструкции, на что нужно обращать внимание при выполнении подобных заданий.
Например: сравнить все слова в ряду: какие буквы повторяются, как изменяется количество букв в словах, принадлежность к части речи, значение слов и т. д.
4. Домашнее задание (3 мин)Придумать как можно больше рядов слов, построенных по разным правилам.
Проверка выполнения этого домашнего задания проводится на уроке русского языка.
5. Упражнение «Проверь себя» (7–8 мин)– Бывают такие буквенные закономерности, когда нужно расшифровать слово, изображённое условными значками. Например, даны слова: пуля, дядя, арка, торт (Учитель записывает слова на доске).
Какое из этих слов зашифровано следующим образом «+ *! *»? («Шифр» записывается на доске.)
– … (дядя, т. к. в слове вторая и четвертая буквы одинаковые)
– А это какое слово: «X # = У»? (Запись на доске.)
– … (Пуля, так как все буквы в слове разные).
На доске открывается несколько рядов слов, нужно выбрать и записать то слово, которое соответствует условным значкам. Возможен вариант выполнения задания, когда все ряды предъявляются не одновременно, а поочередно, по мере их выполнения и проверки.
Примеры рядов закономерностей:
* Х: * стук, кино, крик, няня;
! * = # обед, тара, соус, рама;
?:? = мука, обои, град, лапа;
+? *? лицо, река, желе, окно;
Х = Х О + старт, сосна, ребро, ответ;
* +?? + маска, касса, сумка, лассо;
0 = * Х = слово, олово, казак, шапка, жажда;
= * Х = * тайна, каска, жажда, ванна.
6. Задание на смекалку (7–8 мин)На доске написаны буквенные ряды, представляющие собой не механическое чередование букв алфавита в каком-либо порядке, а первые буквы определённых устойчивых последовательностей. Нужно обнаружить эту последовательность и продолжить ряд.
Примеры рядов:
7. Игра «Да-нетка» (5–6 мин)– Три месяца узник находился в старом и мрачном подвале. В качестве пищи ему давали только с ухой хлеб и воду. Когда его освободили, в его темнице, в углу, оказалось много костей. Откуда они взялись?
(Это были рыбьи кости из ухи.)
Комментарий к ответу: при восприятии задания на слух предлог + существительное «с ухой» сливаются в прилагательное «сухой», которое воспринимается как определение к слову «хлеб». И в таком случае действительно непонятно, откуда появились кости, если были только хлеб и вода.
8. Подведение итогов занятия.Занятие 16
Логические задачи
На доске записана схема «Виды логических задач»
Затем учитель в произвольном порядке показывает на различные виды задач, а дети хором называют их местоположение на схеме: слева, справа, внизу, вверху.
Игра может проходить в быстром темпе на выбывание.
2. Решение логических задач на упорядочение (10 мин)– Сегодня на занятии мы с вами будем учиться решать логические задачи. Логические задачи отличаются от обычных тем, что в них требуется не умение вычислять, а умение рассуждать… Логические задачи бывают разных видов, некоторые из них мы рассмотрим на этом занятии.
Учитель зачитывает текст задачи, дети хором отвечают.
Примеры задач:
• Петя старше Маши, а Маша старше Коли. Кто самый старший?
(Петя.)
• Серёжа выше Наташи, а Оля выше Серёжи. Кто самый высокий?
(Оля.)
• Ваня худее Миши, но толще Андрея. Кто самый худой?
(Андрей.)
• Катя иаее, чем Лиза. Лиза иаее, чем Лена. Кто иаее всех?
(Катя.)
• Прс веселее, чем Лвд. Прс печальнее, чем Ксн. Кто веселее всех?
(Ксн.)
• Вшф клмнее, чем Двт. Жкн клмнее, чем Вшф. Кто клмнее всех?
(Жкн.)
Лошадь ниже, чем кролик. Лошадь выше, чем жираф. Кто выше всех?
(?)
При решении «таинственных» задач (с непонятными словами) дети нередко вначале пытаются выяснить, расшифровать, что значат эти слова. Учитель показывает, что для нахождения ответа это не нужно. Последняя задача – «ловушка»: в ней логические выводы вступают в противоречие с реальностью. При решении подобных задач следует давать два ответа: один – формально-логический, вытекающий из условия; и второй – показывающий ошибочность первого ответа с позиций здравого смысла.
При решении задач на упорядочивание рекомендуется записывать условие со знаками «<» и «>» или использовать схемы. При этом знак «>» обозначает любой превосходящий признак: старше, выше, толще, веселее и т. д.
Далее учитель предлагает решить задачу на упорядочение (заранее написана на доске) и составить алгоритм решения подобных задач.
Задача:
«Ваня старше Пети. Дима младше Коли. Петя старше Коли. Ваня младше Юры. Кто старше всех?»
Вариант алгоритма решения:
1. Записать условие при помощи знаков: В>П, Д<К, П>К, В<Ю.
2. Привести все записи к единому виду: В>П, К>Д, П>К, Ю>В.
3. Расставить по порядку: Ю>В, В>П, П>К, К>Д, или Ю>В>П>К>Д.
4. Ответить на вопрос задачи: Юра – самый старший.
Полученный алгоритм предлагается использовать для самостоятельного решения более сложной задачи на упорядочение.
Задача (заранее написана на доске):
«Возле почты растут 6 деревьев: сосна, берёза, липа, тополь, ель и клён. Какое из деревьев самое высокое и какое самое низкое, если известно, что берёза ниже тополя, липа выше клёна, сосна ниже ели, липа ниже берёзы, сосна выше тополя?» (Ель – самое высокое дерево, клён – самое низкое.)
3. Решение логических задач: родственные отношения (5 мин)Учитель предлагает 5–6 задач «про родственников» (можно в виде упражнения «Проверь себя»).